Babylonia

Babylonia

Babylonia is an ancient country in central-southern Mesopotamia. It had acquired mathematics knowledge that is considered the most advanced in the world at its time (the full scope of Babylonian’s knowledge is still being investigated today) . At the same time the Hanging Gardens of Babylon was admired by the Greeks and they included it as one of the seven wonders of the ancient world. Below is a 19th century colored engraving depicting the Hanging Gardens:

Originally Babylonia was a small state in a minor provincial town called Babylon. People in central Mesopotamia interacted with the Sumerians further south and there were culture exchange between them. The Sumerian language and the native language of people in central Mesopotamia, the Akkadian language, started to influence each other. Many people in Babylon, like people in neighboring areas, were bilingual. Over time, people from other parts of Mesopotamia moved into Babylonia. One group was the Amorite from the northwest. They gained power and became the ruler of Babylon. Below is a map showing the location of Babylon:

Although the territories of Babylon expanded slightly over time, it remained very small and was overshadowed by more powerful neighboring kingdoms such as Assyria in the north and Elam in the east. Oftentimes, Babylonia was a vassal of other kingdoms.

The situation changed during the reign of Hammurabi (1810-1750 BCE). He conducted major building work in Babylon, expanding it from a small town into an important city in the area. Being a very efficient ruler, he established a bureaucracy, with taxation and centralized government. Hammurabi freed Babylon from the ruling kingdom and became an independent state. Hammurabi then systematically conquered southern Mesopotamia. It was only from the time of Hammurabi that southern Mesopotamia acquired the name Babylonia. Below is a map showing the extent of Babylonia at the start (dark brown) and end of Hammurabi’s reign.

One of Hammurabi's most important and lasting works was the compilation of the Babylonian law code, which improved the much earlier codes of Sumer and Assyria. In recognition of his contribution, a relief portrait of Hammurabi was placed over the gallery doors of the House Chamber in the U.S. Capitol.

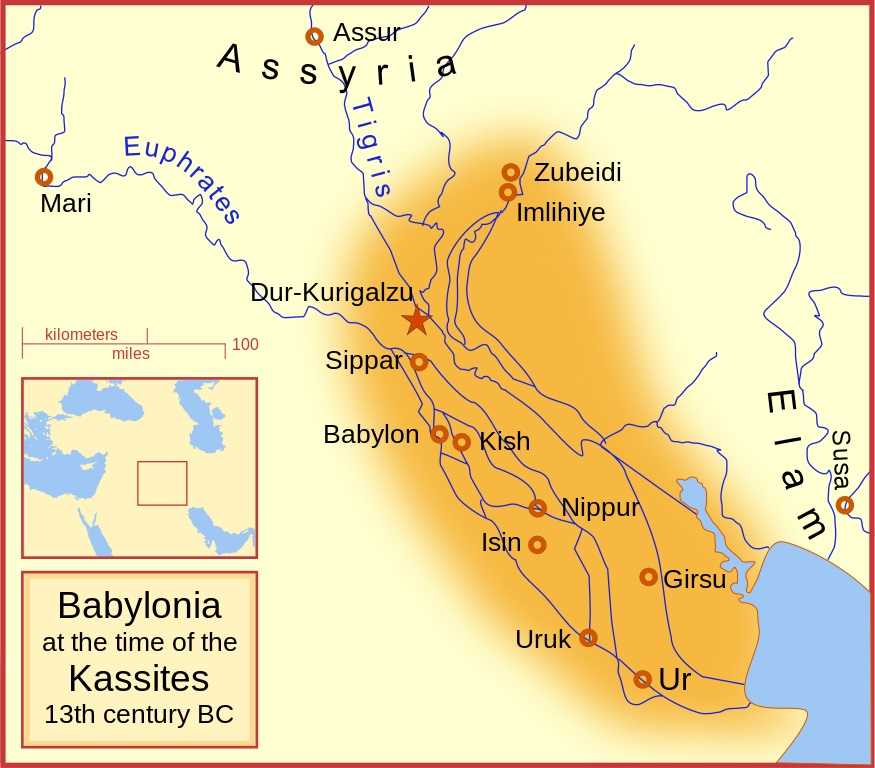
Babylonia’s power declined after the death of Hammurabi. Around 1595 BCE Babylon was sacked by a Hittite king from the north. The Hittites left soon after and another tribe of Babylonian, the Kassites, moved in and ruled the country. The Kassites ruled Babylonia between 1595 and 1155 BCE. Below is a map of Babylonia under the Kassites.

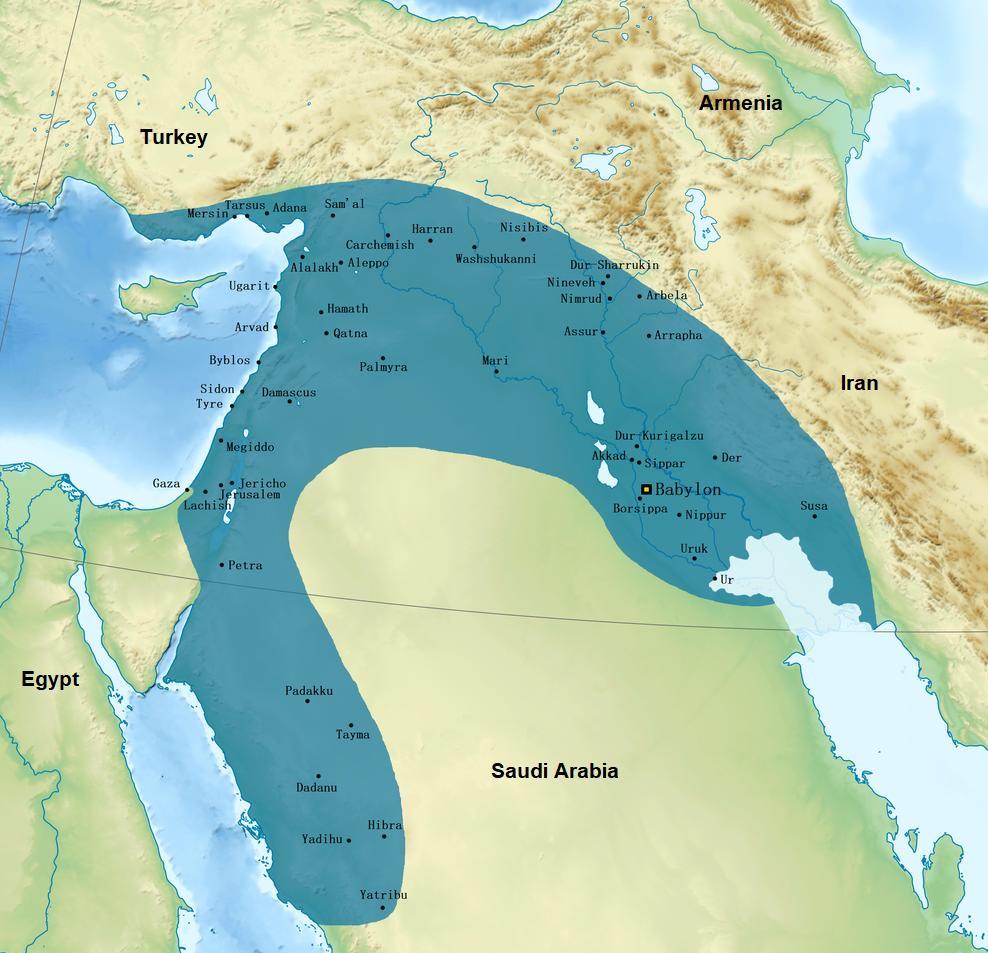
After the Kassites were toppled, Babylonia was ruled by mostly weak rulers. This period came to a close when Babylonia was conquered by Assyria, which ruled between 911-610 BCE. Near the end of Assyrian rule, there were in-fights in Assyria. The Babylonian revolted and formed alliance with external forces to topple the Assyria king. Babylonia became an independent country. Below is a map showing the extent of Babylonia around 550 BCE.

While countries in Mesopotamia were fighting with one another, a new power arose from the East - the Persians. In 539 BCE, Cyrus the Great, the Achaemenid king of Persia, conquered Babylonia and then went on to conquer additional land to became the largest country at that time.

The main legacy of Babylonia is the large number of cuneiform documents it had left behind (see the Sumer page on cuneiform). In particular, there are several hundred cuneiform on astronomy and mathematics. Below is a picture of one of the tablets (YBC 7289) that was used by the Babylonians to calculate the square root of 2:

Below is a picture of a tablet showing a skillfully drawn Babylonia square labyrinth (MS 3194) that needed to follow an algorithm for its construction:

There are many kinds of mathematics related tablets. Examples are

(a) tables (multiplication, division, etc.)
(b) geometry (calculation of triangle, rectangle, trapezoid, circle, etc.).
(c) algebra (calculate square root of 2, cubic and quadratic equations, etc.)
(d) financial (e.g., calculation involving interest rates)
(e) sequences and series

Many of the calculations were related to finding practical solutions in their daily lives. For example, one tablet described a method to compute the weight of a giant object using geometry. Also, there were tablets providing mathematics exercises for students.

Below are some publications on Babylonian mathematics:

A Remarkable Collection of Babylonian Mathematical Texts

Babylonian Mathematics with Special Reference to Recent Discoveries

The Best Known Old Babylonian Tablet?

Babylonian Mathematics

Square Root Approximations in Old Babylonian Mathematics: YBC 7289 in Context

Six More Mathematical Cuneiform Texts in the Schoyen Collection

Quadratic Equations in the Susa Mathematical Text No. 21

On Old Babylonian Mathematical Terminology and its Transformations in the Mathematics of Later Periods

The Antecedents of Old Babylonian Place Notation and the Early History of Babylonian Mathematics

Interest, Price, and Profit: An Overview of Mathematical Economics in YBC 4698

Sequences and Series in Old Babylonian Mathematics

The Babylonians are good astronomers. Below is tablet number 86378 (also called MUL.APIN). The first words of this text are 'Mul Apin' which means 'The Plough' -- a group of seven bright stars which make up part of the constellation called Ursa Major today (this group of stars is also called "the Big Dipper"). MUL.APIN is a form of star catalog and was likely compiled around 1000 BCE. The text lists the names of 66 stars and constellations and further gives a number of indications, such as rising, setting and culmination dates, that help to map out the basic structure of the Babylonian star map.

A portion of the tablet wrote (note: Nisannu, Ajjaru, Simanu, Du'uzu, Abu, and Ululu are name of months in the Babylonian calendar):

"On the 1st of Nisannu the Hired Man becomes visible.
On the 20th of Nisannu the Crook becomes visible.
On the 1st of Ayyaru the Stars become visible.
On the 20th of Ayyaru the Jaw of the Bull becomes visible.
On the 10th of Simanu the True Shepherd of Anu and the Great Twins become visible.
On the 5th of Du'uzu the Little Twins and the Crab become visible.
On the 15th of Du'uzu the Arrow, the Snake, and the Lion become visble; 4 minas is a daytime watch, 2 minas is a nighttime watch.
On the 5th of Abu the Bow and the King become visible.
On the 1st of Ululu [. . . .]
On the 10th of Ululu the star of Eridu and the Raven become visible.
On the 15th of Ululu Shu-pa, Enlil, becomes visible.
On the 25th of Ululu the Furrow becomes visible."

Below are publications on Babylonian astronomy:

The Babylonian Astronomical Compendium MUL.APIN